VGVSBody¶

This abstract class represents a soft body modeled under the Volumetric Geometric Variable Strain (VGVS) approach of [1]. The class implements all the methods required by a Body. Concrete subclasses must define a strain basis 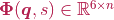$\boldsymbol{\Phi}(\boldsymbol{q}, s) \in \mathbb{R}^{6 \times n}$ such that

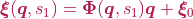
$\boldsymbol{\xi}(\boldsymbol{q}, s_{1}) = \boldsymbol{\Phi}(\boldsymbol{q}, s_{1})\boldsymbol{q} + \boldsymbol{\xi}_{0}$

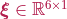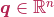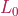where $\boldsymbol{\xi} \in \mathbb{R}^{6 \times 1}$ is the strain, being $\boldsymbol{\xi}_{0}$ its stress-free value, $\boldsymbol{q} \in \mathbb{R}^{n}$ the vector of configuration variables and $s_{1} \in [0, L_{0}]$ the curvilinear abscissa, with $L_{0}$ the body rest length.

Concrete subclasses can also override the radius function to model the body of the radius as follows

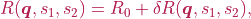
$R(\boldsymbol{q}, s_{1}, s_{2}) = R_{0} + \delta R(\boldsymbol{q}, s_{1}, s_{2}),$

where 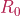$R_{0}$ is the stress-free radius and 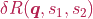$\delta R(\boldsymbol{q}, s_{1}, s_{2})$ models the radius change.

See VPCC2D for a possible implementation.

class VGVSBody¶

Bases: Body

Abstract class modeling a Volumetric continuum under the Geometric Variable Strain (GVS) approach and radius configuration variables. The internal interaction forces are modeled using a linear visco-elastic law. All volume integrals are computed in cylindrical coordinates with a Gaussian quadrature rule.

Constructor Summary

VGVSBody(n, Parameters)¶

Construct a VGVS body.

Parameters:

n (double) – Number of DoF of the body
Parameters ([double], [sym]) – Parameters of the body, specified as $L_{0}, R_{\mathrm{base}}, R_{\mathrm{tip}}, \rho, E, \nu, \eta$ and $N_{\mathrm{Gauss}}$

Property Summary

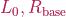Parameters¶: Vector collecting the parameters of the GVS Body as $\mathrm{Parameters} = \left( L_{0} \,\, R_{\mathrm{base}} \,\, R_{\mathrm{tip}} \,\, \rho \,\, E \,\, \nu \,\, \eta \,\, N_{\mathrm{Gauss}} \right)^{T} \in \mathbb{R}^{8 \times 1}$ , where $L_{0}, R_{\mathrm{base}}$ and $R_{\mathrm{tip}}$ denote the body rest length, the base and tip radius, $E$ is the Young modulus, $\nu$ the Poisson ratio, $\eta$ the material damping coefficient, and $N_{\mathrm{Gauss}}$ represents the number of Gaussian points used for the computation of the kinematics and the volume integrals.

VPCC2D